Skew
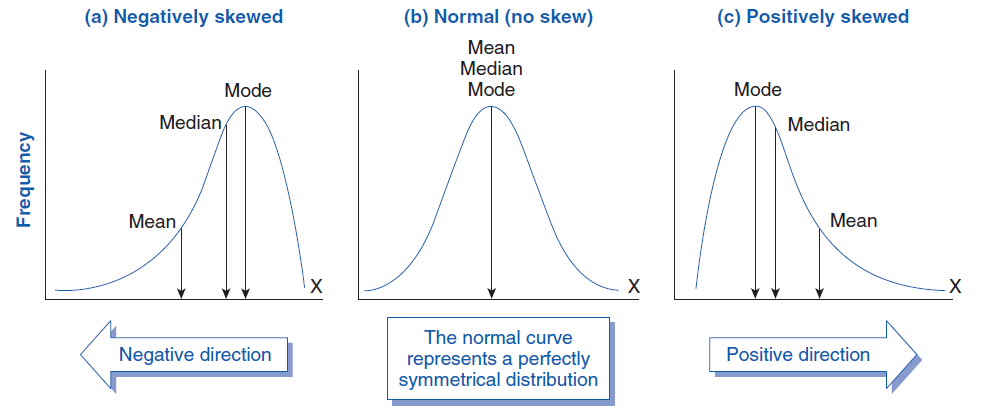
Skewness is a measure of the asymmetry of the distribution of the measurements of a variable relative to its mean. If the distribution of data for a variable stretches toward the right or left tail of the distribution, then the distribution is characterized as skewed. As the data becomes skewed from a normal distribution, the mean loses its ability to provide the best measure of central tendency.
How to I know if my data is skewed?
You’ll calculate skew for the trials for each level of your manipulated variable. So, if you had five levels of manipulation, you’ll calculate skew 5 times - one time each with the data for each level of your manipulated variable.
A negative skewness indicates a greater number of values larger than the mean, whereas a positive skewness indicates a greater number of values smaller than the mean.
The absolute value of the skew number indicates just how skewed the data is. If skewness = 0, the data are perfectly symmetrical. But a skewness of exactly zero is quite unlikely for real-world data, so how can you interpret the skewness number? Hair et al. suggests this rule of thumb:
Any absolute value 2.0 or less is fine for using the mean as your measure of central tendency. If the absolute value is more than 2.0, consider using the median to represent your data.
Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2022). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM) (3 ed.). Thousand Oaks, CA: Sage.
- Use an online SKEW calculator. Here’s a good option. Be sure to include a citation in your paper if you use this tool.
- Use the “SKEW” function in Microsoft Excel. Here’s directions.
- Use the “SKEW” function in Google Sheets. Here’s the directions.
A negative skewness indicates a greater number of values larger than the mean, whereas a positive skewness indicates a greater number of values smaller than the mean.
The absolute value of the skew number indicates just how skewed the data is. If skewness = 0, the data are perfectly symmetrical. But a skewness of exactly zero is quite unlikely for real-world data, so how can you interpret the skewness number? Hair et al. suggests this rule of thumb:
- If skewness is between −.5 and +.5, the distribution is approximately symmetrical.
- If skewness is between −1 and −.5 or between +.5 and +1, the distribution is slightly skewed.
- If skewness is less than −1 or greater than +1, the distribution is moderately skewed but acceptable.
- Skew values beyond −2 and +2 are considered indicative of substantial nonnormality.
Any absolute value 2.0 or less is fine for using the mean as your measure of central tendency. If the absolute value is more than 2.0, consider using the median to represent your data.
Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2022). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM) (3 ed.). Thousand Oaks, CA: Sage.