Chi-Square (X2) Goodness of Fit

Chi-square Goodness of Fit is a statistical test commonly used to compare observed data with data we would expect to obtain.   Were the deviations (differences between observed and expected) the result of chance, or were they due to other factors?  

The chi-squared statistic is a single number that tells you how much difference exists between your observed counts and the counts you would expect if there were no difference at all in the population.  A low value for chi-square means there is little difference between what was observed and what would be expected.  In theory, if your observed and expected values were equal (“no difference”) then chi-square would be zero.  Tip: The Chi-square statistic can only be used on numbers. They can’t be used for percentages, proportions, means or similar statistical value. For example, if you have 10 percent of 200 people, you would need to convert that to a number (20) before you can run a test statistic.

Just like other statistical tests, the Chi-Square Goodness of Fit tests two hypotheses:

Null Hypothesis:
"There is not a significant difference between what was observed and what was expected; any difference between observed and expected is likely due to chance and sampling error."

For example:  

• There is no significant difference between the numbers rolled on the die; the differences seen between numbers may be due to chance and sampling error.

Alternative Hypothesis:
"There is a significant difference between what was observed and what was expected; the differences between observed and expected is likely not due to chance or sampling error."

For example:  

• There is a significant difference between the numbers rolled on the die; the differences seen between numbers are likely not due to chance or sampling error.

How to Calculate a Chi-Square Goodness of Fit

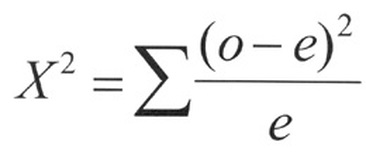
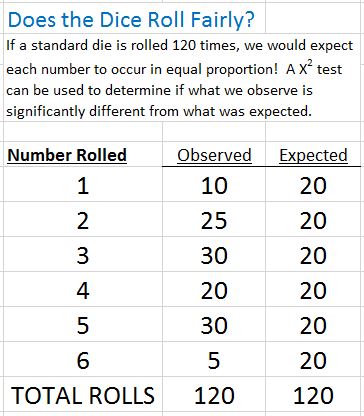
1. The first step in the calculation of an X2 value is to determine the expected numbers.  In genetics, you'd use a Punnett square to determine the theoretical expected values. ​
2. Then, use the formula for each observed and expected category: (O-E)2 / E
3. The results are added together to get a final X2 value.  
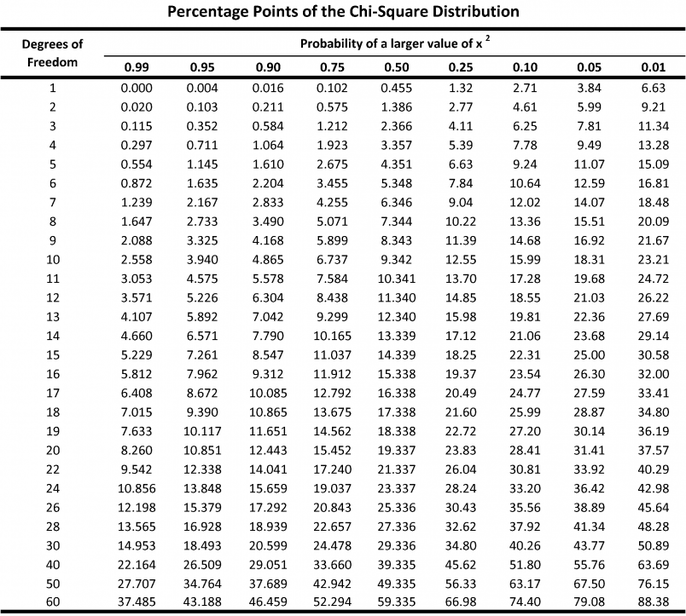
4. ​The calculated X2 value is than compared to the “critical value  X2” found in an X2 distribution table.  

---

• The X2 distribution table represents a theoretical curve of  expected results. ​The expected results are based on DEGREES OF  FREEDOM.  Degrees of Freedom = number of categories – 1. ​

​

• ​The X2 distribution table is organized by the Level of  Significance.  The level of significance is the maximum tolerable probability of accepting a false null hypothesis.  We use 0.05.  

• If our calculated value is lower than the critical value in the table at the 0.05 level of significance, we can accept our null hypothesis and conclude that there is NO significant difference between the observed and expected values. 
• If our calculated value is higher than the critical value in the table at the 0.05 level of significance, we can reject our null hypothesis and conclude that there IS a significant difference between the observed and expected  values.  

Performing a Chi-Square test in Google Sheets

• The formula to  use is =CHITEST(observed_range, expected_range).  Where "observed_range" is the counts associated with each category of data and "expected_range" is the expected counts for each category under the null hypothesis.

Performing a Chi-Square test in Excel 2016

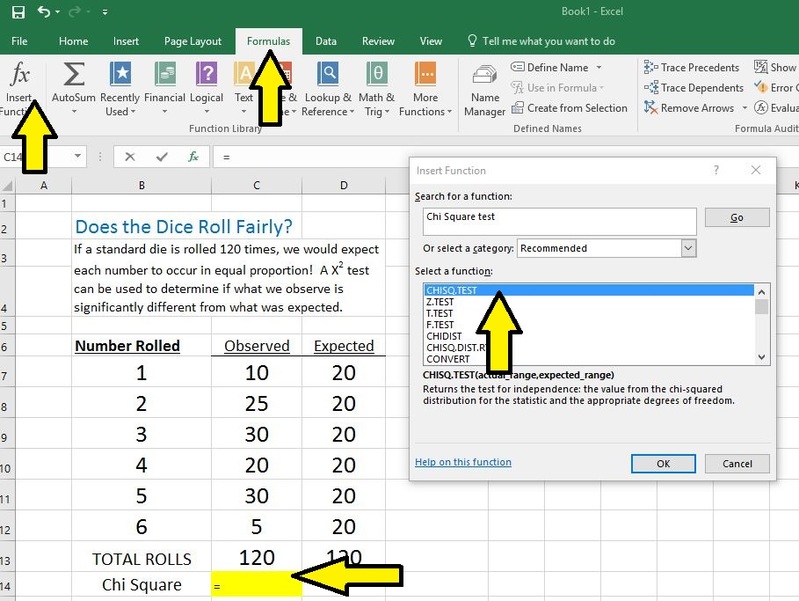
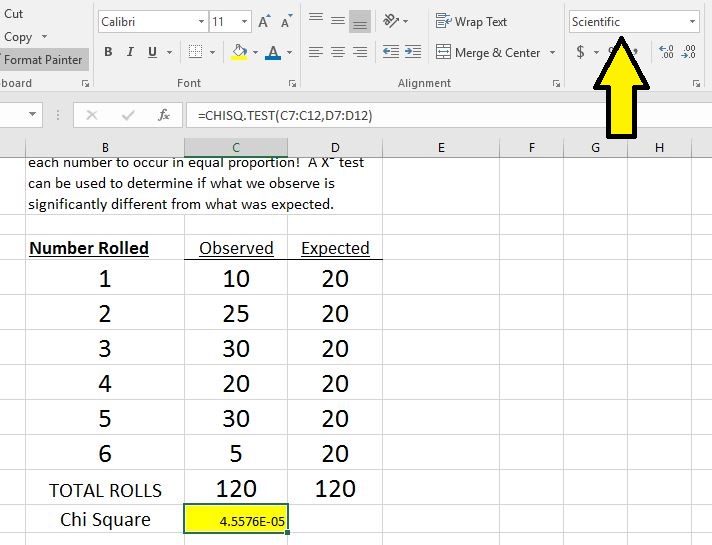
• ​Enter your observed and expected values in columns.
• Click the box in which you want the Chi Square value to be placed
• Select Insert Function from the Formulas tab
• Search for Chi Square test and select the CHISQ.TEST from the menu
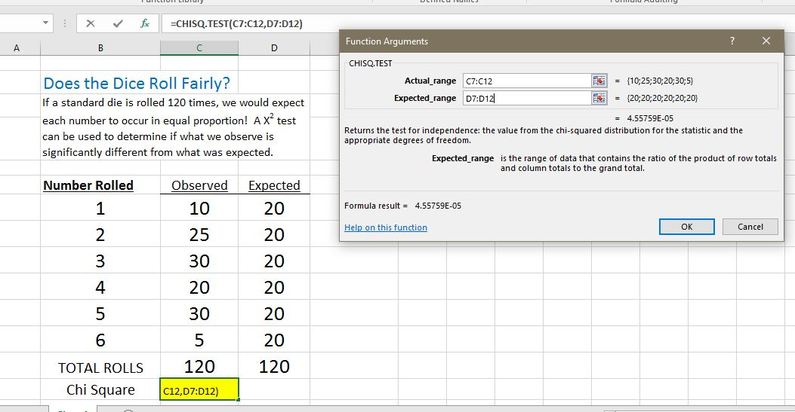
• Hit OK

• Select all of your observed (actual) results for the Actual_range and all of your expected results for the Expected_range.
• Hit OK

• The resulting value is the P value for the Chi-Square  test.  If you don't want it to be in scientific notation, you can change the format of the number by selecting "number"  instead of "scientific."
• If the p-value you get is less than 0.05, reject the null hypothesis  and conclude that there is a significant difference between the observed and expected values.  Likewise, if the p-value is more than 0.05, accept the null hypothesis and conclude that there is no significance difference between the observed and expected. ​

Performing a Chi-Square test with the TI-83/84 

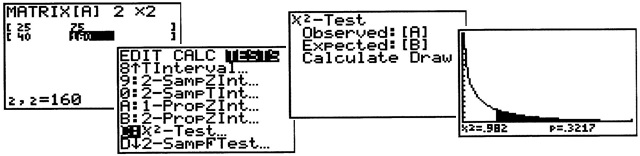
1. ​Press [2nd MATRIX]
2. Select [EDIT - > 1:A]
3. Copy the data by typing in each number and then pressing ENTER
4. Now press STAT. Under the TESTS sub-menu, scroll down and select C:X2 TEST.  Press ENTER.
5. Move the cursor down to DRAW and press ENTER.​
6. If the p-value you get is less than 0.05, reject the null hypothesis  and conclude that there is a significant difference between the observed and expected values.  Likewise, if the p-value is more than 0.05, accept the null hypothesis and conclude that there is no significance difference between the observed and expected. ​